

It is represented in terms of standard deviation. Z score of a value defines how far or close the position of a raw value is from the mean value of the set of data. It is a raw value’s relationship to a set of values. Z score is the position of a single data with respect to its mean value which is defined in terms of standard deviation. More technically it’s a measure of how many standard deviations below or above the population mean a raw score is. between negative infinity and Z).Simply put, a z-score (also called as standard score) gives you an idea of how far from the mean a data point is. This table gives a probability that a statistic is less than Z (i.e. Note that for z = 1, 2, 3, one obtains (after multiplying by 2 to account for the interval) the results f ( z) = 0.6827, 0.9545, 0.9974, If X is a random variable from a normal distribution with mean μ and standard deviation σ, its Z-score may be calculated from X by subtracting μ and dividing by the standard deviation:
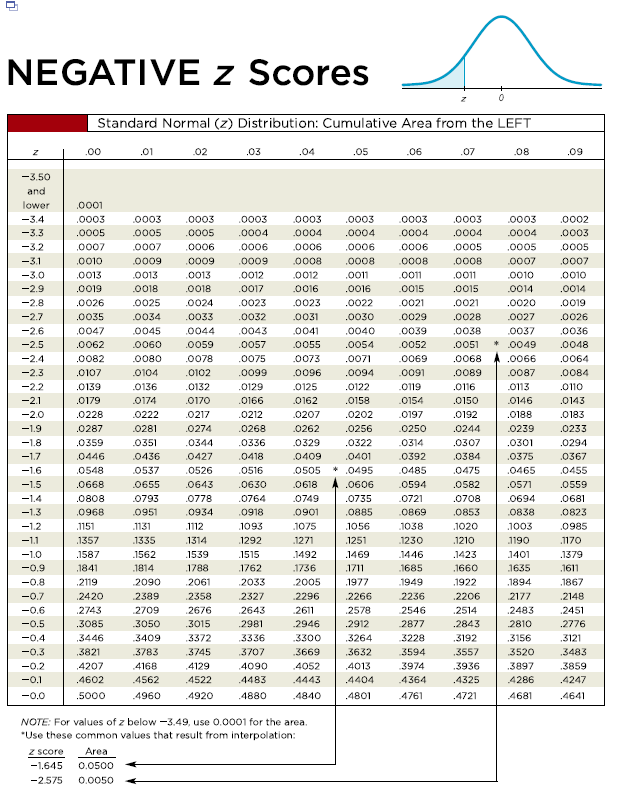
The standard normal distribution, represented by Z, is the normal distribution having a mean of 0 and a standard deviation of 1.
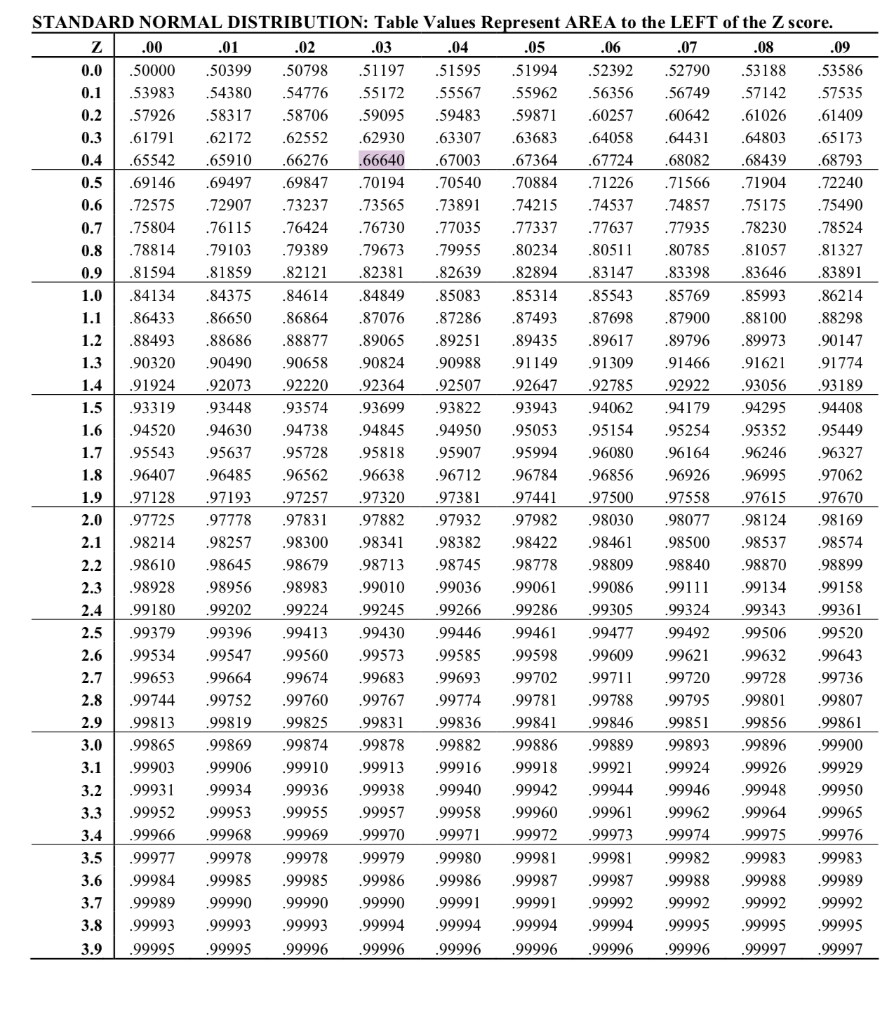
Normal distributions are symmetrical, bell-shaped distributions that are useful in describing real-world data. Since probability tables cannot be printed for every normal distribution, as there are an infinite variety of normal distributions, it is common practice to convert a normal to a standard normal (known as a z-score) and then use the standard normal table to find probabilities. It is used to find the probability that a statistic is observed below, above, or between values on the standard normal distribution, and by extension, any normal distribution. In statistics, a standard normal table, also called the unit normal table or Z table, is a mathematical table for the values of Φ, the cumulative distribution function of the normal distribution. Table of probabilities related to the normal distribution


 0 kommentar(er)
0 kommentar(er)
